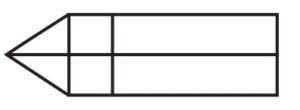
66. नीचे दी गई आकृति में कितने आयत हैं ?
(A) 9
(B) 12
(C) 8
(D) उपर्युक्त में से एक से अधिक
(E) उपर्युक्त में से कोई नहीं
Click To Show Answer
कारण: चित्र में आयतों की संख्या ज्ञात करनी है। चित्र में एक त्रिकोणीय भाग और एक आयताकार भाग है। आयत केवल आयताकार भाग में ही मौजूद हैं।
आयताकार भाग एक क्षैतिज रेखा और एक ऊर्ध्वाधर रेखा द्वारा छोटे वर्गों में विभाजित है। आइए इस भाग में आयतों की संख्या व्यवस्थित तरीके से गिनते हैं।
मान लीजिए कि आयताकार भाग 2×2 छोटे आयतों का ग्रिड है।
1. एकल आयत: 4 छोटे व्यक्तिगत आयत हैं।
2. दो छोटे आयतों को मिलाकर बने आयत:
क्षैतिज रूप से: आसन्न क्षैतिज आयतों के 2 जोड़े हैं।
ऊर्ध्वाधर रूप से: आसन्न ऊर्ध्वाधर आयतों के 2 जोड़े हैं।
3. चार छोटे आयतों को मिलाकर बने आयत:
पूरा 2×2 ग्रिड एक बड़ा आयत बनाता है।
आयतों की कुल संख्या = (1×1 आयतों की संख्या) + (1×2 आयतों की संख्या) + (2×1 आयतों की संख्या) + (2×2 आयतों की संख्या)
आयतों की कुल संख्या = 4 + 2 + 2 + 1 = 9।
आइए 2×2 ग्रिड के लिए सूत्र का उपयोग करके इसे सत्यापित करें, जहाँ आयतों की संख्या $\frac{m(m+1)}{2} \times \frac{n(n+1)}{2}$ द्वारा दी जाती है। इस मामले में, ग्रिड 2×2 है, इसलिए m=2 और n=2।
आयतों की संख्या = $\frac{2(2+1)}{2} \times \frac{2(2+1)}{2} = \frac{2 \times 3}{2} \times \frac{2 \times 3}{2} = 3 \times 3 = 9$
दी गई आकृति में आयतों की संख्या 9 है।
